Efficient approximate square roots and division in Verilog
January 23, 2021
SuperRT uses, for the most part, fairly simple maths operations - integer addition and multiplication - which are natively supported by Verilog (and can be offloaded to DSPs in some cases). There are, however, some places where it inevitably has to do more complex operations - notably divides and square roots (he hardware side avoids the need for any sine/cosine calculations by formatting the incoming data in such a way that the SNES CPU takes those on).
So I needed a way to support these these operations, and to keep the pipeline constraints simple I knew I needed an algorithm that could execute in a fixed number of cycles - so variable-length iterative approaches were out. On the plus side, I could afford to sacrifice a bit of accuracy for speed, and I didn’t need to worry too much about the semantics of invalid/out-of-range inputs as those would (hopefully!) never occur normally.
A quick note: SuperRT was my first FPGA project, and arguably best described as “a massively over-complicated Hello World”. My understanding of Verilog is incomplete at best and most likely downright wrong in at worst, so please take everything I say about it with a pinch of salt. Additions/corrections are gratefully accepted!
I started looking at square root first - for reasons that will become apparent shortly - and after looking around a bit for information on hardware-suitable algorithms and not finding very much guidance, I decided to try some experiments in software first. Based on the “fixed number of cycles” constraint, Newton-Raphson seemed like a good candidate - this is an iterative method where each step can be done with a fixed number of operations, and the number of steps required is determined by the desired output accuracy.
More specifically, this method calculates the reciprocal of the square root of a value val by iteratively computing this formula for step n:
x(n+1) = (x(n) * (1.5 - (val * 0.5 * x(n)^2))
This calculates the reciprocal
1/sqrt(val), but once we have that we can easily calculate the regular square root by multiplying the result by val, thus yieldingval / sqrt(val)which by definition issqrt(val).
Since each step depends on the output of the previous one, we need to “seed” the initial value of x(0) in order to get started. This initial value is a “first guess” at the answer which is then refined with each iteration, and so a precomputed table seemed to be a good approach to take.
I toyed a bit with the idea of using a lookup ROM for this, but it felt like that was probably going to overcomplicate things. Also, a straightforward lookup based on the upper bits of the input value or similar would either need an unreasonably large table or suffer accuracy problems with smaller inputs. Thus, the approach I ended up taking was to use a magnitude-based lookup, where the initial guess is determined by the number of leading zero bits in the input value. That gives us a table which looks like this:
Number of leading zeroes Mid-value Square root
30 6.103516E-05 0.0078125
29 0.0001831055 0.0135316469341319
28 0.0003662109 0.0191366386154936
27 0.0007324219 0.0270632938682637
26 0.001464844 0.0382732772309872
25 0.002929688 0.0541265877365274
24 0.005859375 0.0765465544619743
23 0.01171875 0.108253175473055
22 0.0234375 0.153093108923949
21 0.046875 0.21650635094611
20 0.09375 0.306186217847897
19 0.1875 0.433012701892219
18 0.375 0.612372435695794
17 0.75 0.866025403784439
16 1.5 1.22474487139159
15 3 1.73205080756888
14 6 2.44948974278318
13 12 3.46410161513775
12 24 4.89897948556636
11 48 6.92820323027551
10 96 9.79795897113271
9 192 13.856406460551
8 384 19.5959179422654
7 768 27.712812921102
6 1536 39.1918358845308
5 3072 55.4256258422041
4 6144 78.3836717690617
3 12288 110.851251684408
2 24576 156.767343538123
1 49152 221.702503368816
0 98304 313.534687076247
Source values are in 14 bit fixed-point and signed, and thus 30 is the maximum number of leading zero bits.
The initial square root guesses are calculated as the square root of the mid-point of the range they are used for.
Using this table to get the initial value and then performing two Newton’s method iterations turned out to give just enough accuracy for SuperRT’s purposes - graphing the error (as a percentage of the answer) over the entire input range gives this:
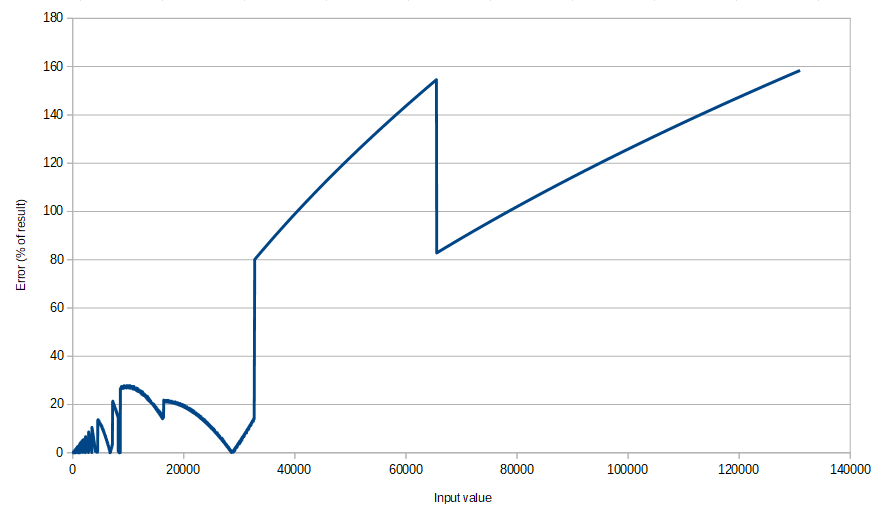
As can be seen, overall error isn’t great (particularly for large numbers), but at the lower end of the range it’s much more reasonable (<1%) and this is where the majority of SuperRT calculations occur:
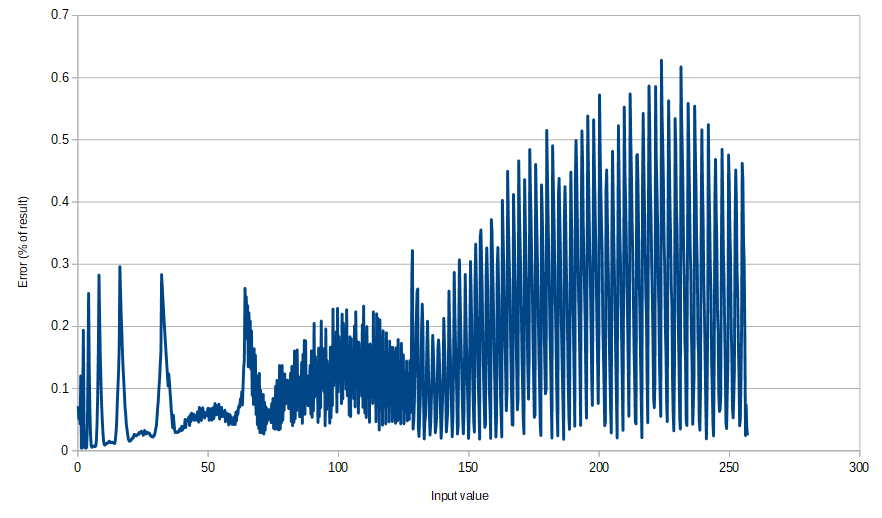
Implemented in Verilog as a big combinatorial function, this solution looks like this:
localparam [31:0] fixedShift = 14; // Left shift factor for fixed point (i.e. how many fractional bits do we have)
localparam signed [31:0] onePointFive = 32'sh00006000; // 1.5f in fixed point
// Fixed-point mul (40-bit internal precision)
function automatic signed [31:0] FixedMul;
input signed [31:0] x;
input signed [31:0] y;
begin
// Sign-extend out to 40 bits and then truncate again afterwards
FixedMul = 32'($signed({{8{x[31]}}, x} * {{8{y[31]}}, y}) >>> fixedShift);
end
endfunction
// Fast fixed-point square root
function automatic signed [31:0] FixedSqrt;
input signed [31:0] sqrtIn; // Input
reg signed [31:0] sqrtFirstGuess; // First guess (table-based)
reg signed [31:0] sqrtIntermediate; // Result of first Newton iteration
reg signed [31:0] sqrtRcpResult; // Result of second Newton iteration
begin
// First-guess lookup based on number of leading zeroes
if (sqrtIn[30]) sqrtFirstGuess = 32'sh00000034;
else if (sqrtIn[29]) sqrtFirstGuess = 32'sh00000049;
else if (sqrtIn[28]) sqrtFirstGuess = 32'sh00000068;
else if (sqrtIn[27]) sqrtFirstGuess = 32'sh00000093;
else if (sqrtIn[26]) sqrtFirstGuess = 32'sh000000d1;
else if (sqrtIn[25]) sqrtFirstGuess = 32'sh00000127;
else if (sqrtIn[24]) sqrtFirstGuess = 32'sh000001a2;
else if (sqrtIn[23]) sqrtFirstGuess = 32'sh0000024f;
else if (sqrtIn[22]) sqrtFirstGuess = 32'sh00000344;
else if (sqrtIn[21]) sqrtFirstGuess = 32'sh0000049e;
else if (sqrtIn[20]) sqrtFirstGuess = 32'sh00000688;
else if (sqrtIn[19]) sqrtFirstGuess = 32'sh0000093c;
else if (sqrtIn[18]) sqrtFirstGuess = 32'sh00000d10;
else if (sqrtIn[17]) sqrtFirstGuess = 32'sh00001279;
else if (sqrtIn[16]) sqrtFirstGuess = 32'sh00001a20;
else if (sqrtIn[15]) sqrtFirstGuess = 32'sh000024f3;
else if (sqrtIn[14]) sqrtFirstGuess = 32'sh00003441;
else if (sqrtIn[13]) sqrtFirstGuess = 32'sh000049e6;
else if (sqrtIn[12]) sqrtFirstGuess = 32'sh00006882;
else if (sqrtIn[11]) sqrtFirstGuess = 32'sh000093cd;
else if (sqrtIn[10]) sqrtFirstGuess = 32'sh0000d105;
else if (sqrtIn[9]) sqrtFirstGuess = 32'sh0001279a;
else if (sqrtIn[8]) sqrtFirstGuess = 32'sh0001a20b;
else if (sqrtIn[7]) sqrtFirstGuess = 32'sh00024f34;
else if (sqrtIn[6]) sqrtFirstGuess = 32'sh00034417;
else if (sqrtIn[5]) sqrtFirstGuess = 32'sh00049e69;
else if (sqrtIn[4]) sqrtFirstGuess = 32'sh0006882f;
else if (sqrtIn[3]) sqrtFirstGuess = 32'sh00093cd3;
else if (sqrtIn[2]) sqrtFirstGuess = 32'sh000d105e;
else if (sqrtIn[1]) sqrtFirstGuess = 32'sh001279a7;
else sqrtFirstGuess = 32'sh00200000;
// Newton's method - x(n+1) =(x(n) * (1.5 - (val * 0.5f * x(n)^2))
// First iteration
sqrtIntermediate = FixedMul(sqrtFirstGuess, onePointFive - FixedMul(sqrtIn >>> 1, FixedMul(sqrtFirstGuess, sqrtFirstGuess)));
// Second iteration
sqrtRcpResult = FixedMul(sqrtIntermediate, onePointFive - FixedMul(sqrtIn >>> 1, FixedMul(sqrtIntermediate, sqrtIntermediate)));
// Convert 1/sqrt(x) to sqrt(x)
FixedSqrt = FixedMul(sqrtRcpResult, sqrtIn);
end
endfunction
…or, in a pipeline-friendly 4-cycle-latency, 1-cycle-throughput form:
localparam [31:0] fixedShift = 14; // Left shift factor for fixed point (i.e. how many fractional bits do we have)
localparam signed [31:0] onePointFive = 32'sh00006000; // 1.5f in fixed point
// Fixed-point mul (40-bit internal precision)
function automatic signed [31:0] FixedMul;
input signed [31:0] x;
input signed [31:0] y;
begin
// Sign-extend out to 40 bits and then truncate again afterwards
FixedMul = 32'($signed({{8{x[31]}}, x} * {{8{y[31]}}, y}) >>> fixedShift);
end
endfunction
// Pipelined clocked square root
module FixedSqrtClocked(
input wire clock,
input wire signed [31:0] sqrtIn, // Input
output wire signed [31:0] result); // Result
// Cycle 1
always @(posedge clock) begin
c2_sqrtIn <= sqrtIn;
// First-guess lookup based on number of leading zeroes
if (sqrtIn[30]) c2_sqrtFirstGuess <= 32'sh00000034;
else if (sqrtIn[29]) c2_sqrtFirstGuess <= 32'sh00000049;
else if (sqrtIn[28]) c2_sqrtFirstGuess <= 32'sh00000068;
else if (sqrtIn[27]) c2_sqrtFirstGuess <= 32'sh00000093;
else if (sqrtIn[26]) c2_sqrtFirstGuess <= 32'sh000000d1;
else if (sqrtIn[25]) c2_sqrtFirstGuess <= 32'sh00000127;
else if (sqrtIn[24]) c2_sqrtFirstGuess <= 32'sh000001a2;
else if (sqrtIn[23]) c2_sqrtFirstGuess <= 32'sh0000024f;
else if (sqrtIn[22]) c2_sqrtFirstGuess <= 32'sh00000344;
else if (sqrtIn[21]) c2_sqrtFirstGuess <= 32'sh0000049e;
else if (sqrtIn[20]) c2_sqrtFirstGuess <= 32'sh00000688;
else if (sqrtIn[19]) c2_sqrtFirstGuess <= 32'sh0000093c;
else if (sqrtIn[18]) c2_sqrtFirstGuess <= 32'sh00000d10;
else if (sqrtIn[17]) c2_sqrtFirstGuess <= 32'sh00001279;
else if (sqrtIn[16]) c2_sqrtFirstGuess <= 32'sh00001a20;
else if (sqrtIn[15]) c2_sqrtFirstGuess <= 32'sh000024f3;
else if (sqrtIn[14]) c2_sqrtFirstGuess <= 32'sh00003441;
else if (sqrtIn[13]) c2_sqrtFirstGuess <= 32'sh000049e6;
else if (sqrtIn[12]) c2_sqrtFirstGuess <= 32'sh00006882;
else if (sqrtIn[11]) c2_sqrtFirstGuess <= 32'sh000093cd;
else if (sqrtIn[10]) c2_sqrtFirstGuess <= 32'sh0000d105;
else if (sqrtIn[9]) c2_sqrtFirstGuess <= 32'sh0001279a;
else if (sqrtIn[8]) c2_sqrtFirstGuess <= 32'sh0001a20b;
else if (sqrtIn[7]) c2_sqrtFirstGuess <= 32'sh00024f34;
else if (sqrtIn[6]) c2_sqrtFirstGuess <= 32'sh00034417;
else if (sqrtIn[5]) c2_sqrtFirstGuess <= 32'sh00049e69;
else if (sqrtIn[4]) c2_sqrtFirstGuess <= 32'sh0006882f;
else if (sqrtIn[3]) c2_sqrtFirstGuess <= 32'sh00093cd3;
else if (sqrtIn[2]) c2_sqrtFirstGuess <= 32'sh000d105e;
else if (sqrtIn[1]) c2_sqrtFirstGuess <= 32'sh001279a7;
else c2_sqrtFirstGuess <= 32'sh00200000;
end
reg signed [31:0] c2_sqrtIn;
reg signed [31:0] c2_sqrtFirstGuess; // First guess (table-based)
// Cycle 2
always @(posedge clock) begin
// Newton's method - x(n+1) =(x(n) * (1.5 - (val * 0.5f * x(n)^2))
// First iteration
c3_sqrtIntermediate <= FixedMul(c2_sqrtFirstGuess, sqrt_onePointFive - FixedMul(c2_sqrtIn >> 1, FixedMul(c2_sqrtFirstGuess, c2_sqrtFirstGuess)));
c3_sqrtIn <= c2_sqrtIn;
end
reg signed [31:0] c3_sqrtIn;
reg signed [31:0] c3_sqrtIntermediate; // Result of first Newton iteration
// Cycle 3
always @(posedge clock) begin
// Second iteration
c4_sqrtRcpResult <= FixedMul(c3_sqrtIntermediate, sqrt_onePointFive - FixedMul(c3_sqrtIn >> 1, FixedMul(c3_sqrtIntermediate, c3_sqrtIntermediate)));
c4_sqrtIn <= c3_sqrtIn;
end
reg signed [31:0] c4_sqrtIn;
reg signed [31:0] c4_sqrtRcpResult; // Result of second Newton iteration
// Cycle 4
always @(posedge clock) begin
if (c4_sqrtIn == 'h0) begin
result <= 32'h0;
end else begin
// Convert 1/sqrt(x) to sqrt(x)
result <= FixedMul(c4_sqrtRcpResult, c4_sqrtIn);
end
end
I actually tried two variants of the initial lookup code - the version seen here, and what felt like a more “idiomatic Verilog” version using a case statement, as follows:
unique casez(sqrtIn)
32'sb?1??????????????????????????????: c2_sqrtFirstGuess <= 32'sh00000034;
32'sb?01?????????????????????????????: c2_sqrtFirstGuess <= 32'sh00000049;
32'sb?001????????????????????????????: c2_sqrtFirstGuess <= 32'sh00000068;
32'sb?0001???????????????????????????: c2_sqrtFirstGuess <= 32'sh00000093;
32'sb?00001??????????????????????????: c2_sqrtFirstGuess <= 32'sh000000d1;
32'sb?000001?????????????????????????: c2_sqrtFirstGuess <= 32'sh00000127;
32'sb?0000001????????????????????????: c2_sqrtFirstGuess <= 32'sh000001a2;
32'sb?00000001???????????????????????: c2_sqrtFirstGuess <= 32'sh0000024f;
32'sb?000000001??????????????????????: c2_sqrtFirstGuess <= 32'sh00000344;
32'sb?0000000001?????????????????????: c2_sqrtFirstGuess <= 32'sh0000049e;
32'sb?00000000001????????????????????: c2_sqrtFirstGuess <= 32'sh00000688;
32'sb?000000000001???????????????????: c2_sqrtFirstGuess <= 32'sh0000093c;
32'sb?0000000000001??????????????????: c2_sqrtFirstGuess <= 32'sh00000d10;
32'sb?00000000000001?????????????????: c2_sqrtFirstGuess <= 32'sh00001279;
32'sb?000000000000001????????????????: c2_sqrtFirstGuess <= 32'sh00001a20;
32'sb?0000000000000001???????????????: c2_sqrtFirstGuess <= 32'sh000024f3;
32'sb?00000000000000001??????????????: c2_sqrtFirstGuess <= 32'sh00003441;
32'sb?000000000000000001?????????????: c2_sqrtFirstGuess <= 32'sh000049e6;
32'sb?0000000000000000001????????????: c2_sqrtFirstGuess <= 32'sh00006882;
32'sb?00000000000000000001???????????: c2_sqrtFirstGuess <= 32'sh000093cd;
32'sb?000000000000000000001??????????: c2_sqrtFirstGuess <= 32'sh0000d105;
32'sb?0000000000000000000001?????????: c2_sqrtFirstGuess <= 32'sh0001279a;
32'sb?00000000000000000000001????????: c2_sqrtFirstGuess <= 32'sh0001a20b;
32'sb?000000000000000000000001???????: c2_sqrtFirstGuess <= 32'sh00024f34;
32'sb?0000000000000000000000001??????: c2_sqrtFirstGuess <= 32'sh00034417;
32'sb?00000000000000000000000001?????: c2_sqrtFirstGuess <= 32'sh00049e69;
32'sb?000000000000000000000000001????: c2_sqrtFirstGuess <= 32'sh0006882f;
32'sb?0000000000000000000000000001???: c2_sqrtFirstGuess <= 32'sh00093cd3;
32'sb?00000000000000000000000000001??: c2_sqrtFirstGuess <= 32'sh000d105e;
32'sb?000000000000000000000000000001?: c2_sqrtFirstGuess <= 32'sh001279a7;
default: c2_sqrtFirstGuess <= 32'sh00200000;
endcase
Both of these produce identical results, but interestingly synthesize to very different RTL - the if statements produce a linear cascade of of tests that broadly mirror the Verilog structure, like this:

Whilst the case statement produces a big network of gates that generate each bit of the output separately:

The two have broadly similar resource requirements (402 ALUTs and 190 registers for the case statement vs 437 ALUTs and 184 registers for the if version) - SuperRT uses the if version for no particular reason other than that it was the one I wrote first.
This code calculates 1/sqrt(val), and from there sqrt(val), but it can also be used to calculate 1/val simply by taking the square of the result, thus giving (1/sqrt(val))^2 and yielding 1/val. Once we have a means of calculating 1/val, division becomes a simple question of taking the reciprocal of the divider and then multiplying.
Just in case anyone happens upon this and wants to use any of the code in this article in their own project (bearing in mind the warning at the top of this page about my Verilog skills!), please feel free to do so - for the sake of avoiding any confusion, I’ll officially put the code snippets here under the 0BSD license:
Copyright © 2021 by Ben Carter ben@shironekolabs.comPermission to use, copy, modify, and/or distribute this software for any purpose with or without fee is hereby granted.
THE SOFTWARE IS PROVIDED “AS IS” AND THE AUTHOR DISCLAIMS ALL WARRANTIES WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.