The Evaluation Stack

A concept which took me a little while to get my head around the first time I encountered it in the CLR is that of the “evaluation stack”, so I thought I’d write a little bit to summarise how it works (or, well, how I think it works, which may be slightly different - let me know if I’ve got anything wrong!).

In terms of how they execute code, the vast majority of CPUs are “register-based”, which is to say that instructions reference data stored in a fixed number of registers held within the chip itself. Some architectures (such as x86) also provide limited functionality for manipulating data in memory directly, but others (such as ARM) only provide arithmetic operations upon registers, requiring programs to load the data they want into them and then store the results back out again afterwards.

In contrast, MSIL - the bytecode used by the CLR - is a “stack based” system. All instructions work on data stored on a virtual stack - so, for example, an ADD instruction pops the top two values from the stack, and then pushes a single result value back onto it. Data read from memory is pushed onto the stack, and similarly storing data back to memory pops it from the stack as it does so.

In some ways, this effectively makes MSIL a form of encoding for Reverse Polish Notation (RPN), which is a mathematical notation where operations are performed in order on a notional stack.

At first glance, this may seem limiting - after all, a modern CPU generally provides a reasonably large register file and instructions that can freely access it so that, for example, an ADD instruction can add values from any two registers and write the result back to any other. This makes it easier to keep data stored in registers and avoid expensive load/store operations.

However, there are two interesting facts to consider here. Firstly, MSIL is designed primarily to be generated by compilers, not humans - this has implications we will discuss a little later. And secondly, MSIL is not intended to be executed directly - it is designed to be JITed into native code for one any number of actual processors. Thus, there is less need to emphasize such optimisations, as they can be performed later (at the JIT stage).

In fact, attempting to optimise the code earlier may actually be counter-productive. Consider that across the many target processors MSIL is ultimately aiming at, the register file sizes can differ wildly, not to mention that the registers themselves can be of varying widths or be specialised for certain data types. Thus, if MSIL was register-based, there would need be a choice made as to how many registers to provide of each type - but if that number is fewer than exist on the eventual target hardware it will be underutilised, whilst if it is greater the JIT will need to jump through hoops to accomodate them, potentially spilling data to memory and generally reducing the quality of the generated code.

There is, it has to be said, a more generic solution to these problems - MSIL could simply specify a very large number of registers, and then the JIT could perform data flow analysis to reduce this number to the quantity available on the target hardware. However, this approach has considerable drawbacks - firstly that underutilisation can still occur if in the future some hardware appears with more than the specified register count, and secondly that performing register allocation (to turn the compiler’s internal representation of data flow into register-based bytecode) and then data flow analysis to turn that back into a representation of data flow again during the JIT phase is a lot of effort to essentially achieve nothing.

So MSIL skips all of this by using a stack. The “evaluation stack”, as it is known, does not even need to exist in memory during execution - rather, it is a conceptual construct that defines how data flows between instructions.

This is achieved by defining the evaluation stack purely in terms of PUSH and POP operations. Unlike the somewhat more messy callstack that virtually all software uses to track return addresses, function parameters and the like, there is no way to “peek” at a value without also removing it, or manipulate an item which is not at the top of the stack.

Thus, each stack entry is written to exactly once, and read exactly once. And as each MSIL instruction pops a number of items from the stack and then pushes some back, each stack entry uniquely ties two (or more) instructions together - one that writes it, and then another that reads it. The “(or more)” refers to the case where there is a conditional branch in the code - during execution the stack entry is written and read once, but there can be several “candidate” instructions that may do those operations depending on which branches are taken.

You may well at this point be thinking that method calls complicate things, as the LDARG family of instructions allow access to values at arbitrary points on the stack. However, if conceptually you regard method calls as popping all of their arguments (and storing them elsewhere), executing the method code and then finally pushing a return value (also stored elsewhere in the interim), this complexity disappears - from the model, at least!

So a stack entry is written exactly once, and read exactly once - that makes them a subset of SSA (Single Statement Assignment) form. The idea behind SSA form is that makes reasoning about data flow in tools such as compilers much simpler by removing the notion of variables being reassigned - each variable in an SSA notation program can only be assigned a value once, after which it is fixed. Data flow branches are handled using special “phi” operators which select one of a number of candidate variables to assign to a new one.

So the evaluation stack notation has a clear link to SSA, which is in turn very commonly used in compilers. But as a subset of valid SSA (remember that in a stack you can only manipulate the topmost value, whereas SSA itself has no such constraint), it isn’t immediately obvious how this is useful - a compiler cannot directly translate arbitrary SSA into stack operations.

This is where the notion of expression trees comes in. Expression trees are a way of representing mathematical expressions in the form of a tree where each leaf node is in input value, and each non-leaf node takes one or more inputs nodes, performs an operation on them, and then passes the result “up” the tree to another node. Eventually, at the root of the tree only one node is left, and the output of that is the answer.

So, for example, the expression (3 + 4) * (10 - (5 + 2)) can be turned into the following tree:

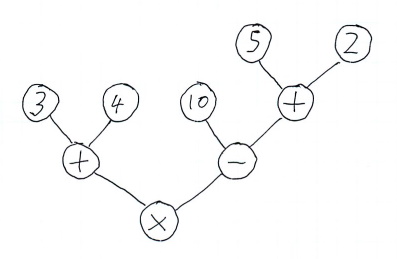
(the actual process for doing so is a bit of a tangent so I won’t go into it here, but suffice to say it is relatively straightforward - The shunting yard algorithm is a good point to start reading if you’re interested)

As can be seen from the diagram, the 3 and 4 nodes are linked to a node that adds them, as are the 5 and 2 nodes. Then the 10 node is linked via a subtraction to the result of the 5+2 calculation, and the result of that is then linked to a multiply node that combines it with the original 3+4 result to produce the answer.

Expression trees can be extended to capture conditionals, and even flow structures such as loops, at which point they start to morph into a more general-purpose representation of code. Some compilers use such trees to store and manipulate the entirety of methods or other logical code blocks.

Expression trees are useful for a number of reasons - for example, if the compiler sees that both of the inputs to a node are constants, it can pre-compute the answer and then substitute a constant node in place of the original operation without affecting the semantics of the tree as a whole. What’s more, this operation can be repeated recursively - in the case of the example tree here eventually removing everything and leaving only a single constant node with the answer (21) in it.

They are also easy to turn into linear code for execution - the compiler simply has to start at the leaf nodes and emit instructions to perform the operations for each, removing the nodes after doing so (thus exposing new leaf nodes to emit), and repeating the process until nothing is left. This approach is guaranteed to produce instructions that evaluate values in the correct order, but it also has one other very useful benefit - as long as it is slightly careful about the order in which it traverses the tree, the compiler can use a stack to keep track of all the intermediate values without ever having to shuffle them around.

The theory behind this is simple - all the compiler has to do is perform a depth-first traversal of the tree. The result of this is can be expressed intuitively as follows - the stack always holds intermediate results such that the most recent one is at the top (from the definition of a stack), whilst a depth-first traversal means that the operands needed for any given operation are always the most recently added unused values. And since a pure push/pop stack can by definition only contain unused values, every operation we encounter in our traversal can simply pop the values it needs.

To write it out in longhand for the expression above, performing a depth-first traversal (going left-right between nodes of equal depth) yields the following instruction sequence (values in []s represent the stack contents):

[]
Load constant 3
[3]
Load constant 4
[3, 4]
Add (3 + 4 = 7)
[7]
Load constant 5
[7, 5]
Load constant 2
[7, 5, 2]
Add (5 + 2 = 7)
[7, 7]
Load constant 10
[7, 7, 10]
Subtract (10 - 7 = 3)
[7, 3]
Multiply (7 * 3 = 21)
[21]

And this notation based on stack operations is exactly what MSIL uses - not only is it easy for a compiler to generate from an expression tree, but it is also trivial to turn back into one - simply look at the stack entry input/outputs for each instruction and link the nodes together to get back to the original expression tree format. In essence, it is less like a “real” stack and more a convenient syntax for encoding expression trees so that the compiler can directly pass them to the JIT (which then uses that notation to perform register allocation for the target hardware).

And so this ties into our other reason why a stack-based model is desirable - whilst a register-based model is more flexible and easier for humans to write efficient code with, if you assume that the vast majority of code will in fact be generated by a compiler via expression trees, that flexibility is actually not particularly relevant.

There is, of course, another use of registers aside from expression evaluation - holding the values of frequently-used variables. MSIL simply chooses to abstract this out - the evaluation stack is purely for intermediate results, and the decision to place a variable in a register for fast access is made instead by the JIT as a separate consideration.

This is one of the reasons why the evaluation stack has certain constraints placed on it - most notably, that it must always contain the same number (and types) of entries regardless of how a instruction was reached. So if code contains branches, when those branches re-converge each must generate the same stack layout.

If this were not the case, it would be possible for the same MSIL instruction to do different things depends on how it was reached (see my previous post for a description of how MSIL instructions use context from the stack). But the cleverness does not stop there - by constraining the stack behaviour (and adding certain rules about branches and execution flow when exceptions occur), MSIL ensures that the stack layout at any point in a method can be determined with a simple linear scan from top to bottom. In other words, there is no need to perform any kind of execution flow analysis - the JIT can simply walk though a method once linearly and calculate all of the type information and data flow necessary to generate an appropriate internal representation.

So whilst at first the evaluation stack may seem like a strange beast, it’s actually a very smart way of efficiently transferring information from the compiler to the JIT. The resulting form is both convenient for the tools and - since it acts and reads much like regular assembly language - easy for humans to conceptualise and reason about.